Allgemeines zu Zahlen (Dezimal, Binär, Hexadezimal)

Dezimalsystem (Basis 10)

Das Dezimalsystem ist das am häufigsten verwendete Zahlensystem und basiert auf der Basis 10. Es verwendet die Ziffern 0 bis 9.

Beispiel: 156 im Dezimalsystem bedeutet:

1 * 10^2 + 5 * 10^1 + 6 * 10^0 = 100 + 50 + 6 = 156

Binärsystem (Basis 2)

Das Binärsystem verwendet die Basis 2 und verwendet nur zwei Ziffern: 0 und 1. Dieses System wird intern in Computern verwendet, da es sich leicht mit elektronischen Schaltern darstellen lässt.

BIT	...	11	10	9	8	7	6	5	4	3	2	1
Wert	...	1024	512	256	128	64	32	16	8	4	2	1
Exp.	...	2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0

Beispiel: 1010 im Binärsystem bedeutet:

1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 0 * 2^0 = 8 + 0 + 2 + 0 = 10 (dezimal)

Hexadezimalsystem (Basis 16)

Das Hexadezimalsystem verwendet die Basis 16 und verwendet die Ziffern 0 bis 9 sowie die Buchstaben A bis F, um die Werte 10 bis 15 darzustellen. Dieses System wird oft in der Programmierung verwendet, um binäre Zahlen kompakt darzustellen.

Hexadezimal	Dezimal
0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
A	10
B	11
C	12
D	13
E	14
F	15

Beispiel: 1A3F im Hexadezimalsystem bedeutet:

1 * 16^3 + A * 16^2 + 3 * 16^1 + F * 16^0
1 * 4096 + 10 * 256 + 3 * 16 + 15 * 1
4096 + 2560 + 48 + 15 = 6719 (dezimal)

Umrechnung zwischen Zahlensystemen

Dezimal zu Binär

Um eine Dezimalzahl ins Binärsystem umzurechnen, dividiert man die Zahl wiederholt durch 2 und notiert den Rest. Die Binärzahl ergibt sich aus den Resten, aufgeschrieben in umgekehrter Reihenfolge.

Beispiel: Dezimalzahl 13

13 ÷ 2 = 6 Rest 1
6 ÷ 2 = 3 Rest 0
3 ÷ 2 = 1 Rest 1
1 ÷ 2 = 0 Rest 1

Binärzahl: 1101

Binär zu Dezimal

Um eine Binärzahl ins Dezimalsystem umzurechnen, multipliziert man jede Ziffer mit 2 hoch der Position (von rechts beginnend mit 0) und summiert die Ergebnisse.

Beispiel: Binärzahl 1011

1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0
8 + 0 + 2 + 1 = 11 (dezimal)

Dezimal zu Hexadezimal

Um eine Dezimalzahl ins Hexadezimalsystem umzurechnen, dividiert man die Zahl wiederholt durch 16 und notiert den Rest. Die Hexadezimalzahl ergibt sich aus den Resten, aufgeschrieben in umgekehrter Reihenfolge.

Beispiel: Dezimalzahl 255

255 ÷ 16 = 15 Rest 15 (F)
15 ÷ 16 = 0 Rest 15 (F)
Hexadezimalzahl: FF

Hexadezimal zu Dezimal

Um eine Hexadezimalzahl ins Dezimalsystem umzurechnen, multipliziert man jede Ziffer mit 16 hoch der Position (von rechts beginnend mit 0) und summiert die Ergebnisse.

Beispiel: Hexadezimalzahl 1C

1 * 16^1 + C * 16^0
1 * 16 + 12 * 1
16 + 12 = 28 (dezimal)

Anwendung in der Assemblerprogrammierung

In der Assemblerprogrammierung, insbesondere auf ARM64, wird oft die Hexadezimaldarstellung verwendet, weil sie eine kompakte Art und Weise darstellt, binäre Daten anzugeben und zu lesen.

Hier ist ein kurzes Beispiel eines ARM64-Assemblercodes:

.global _start

.section .data
    num:    .word   0x0a       // Hexadezimalzahl für 10 (dezimal)

.section .text
_start:
    // Lade die Hexadezimalzahl in ein Register
    ldr x0, =num
    ldr w1, [x0]

    // Beenden des Programms (Exit System Call)
    mov x8, #93       // Syscall für exit auf ARM64
    svc 0

In diesem Beispiel wird die Dezimalzahl 10 in hexadezimaler Darstellung (0x0A) in einem Datenbereich gespeichert und dann in ein Register geladen.

Verwendung des GDBs um dieses Beispiel nachvoll zu ziehen

Kompiliert wird dieses Program mit folgenden Befehlen:

as -o hex.o -g hex.S
ld -o hex -g hex.o

Mit folgenden Befehl wird GDB gestartet:

gdb hex

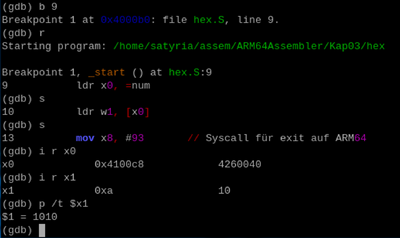
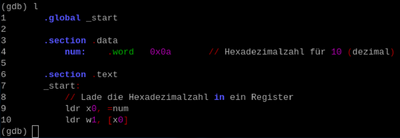
Mit list (l) wird der Source-Code angezeigt:

Der erste Befehl, der uns interessiert ist in der Zeile 9. Mit b 9 (breake 9) setzen wir dort einen Breakpoint. Mit dem Befehl r (run) starten wir das Programm. Unser Programm bleibt beim Breakpoint stehen und der eigentlich erste Befehl, den wir als erstes untersuchen wollen, wurde noch nicht ausgeführt. Mit einem step (s) lassen wir diesen Befehl ausführen und mit einem 2. step auch noch den nächsten. Nun können wir die Register x0 und x1 untersuchen. Mit info reg x0 (i r x0) wird der Inhalt von x0 angezeigt. Dies ist ein Zeiger auf die Variable "num". Mit ldr w1,[x0] wird der Inhalt aus dem Speicher, auf den der Zeiger aus x0 zeigt nach w1 kopiert. Mit i r x1 lassen wir den Inhalt aus x1 anzeigen.

Mit p /t $x1 lassen wir uns den Wert Binär anzeigen.